Новое семейство решений уравнений Максвелла
Международная научная группа во главе с Хридешем Кедиа (Hridesh Kedia) из Чикагского университета (США) получила новые и весьма необычные решения уравнения Максвелла, считая к тому же, что они реализуемы на практике. Учёные обнаружили совершенно новое семейство решений уравнений Максвелла, позволяющее создавать узлы на поверхности тора из световых пучков. Более того, одно из представленных решений включает линии магнитного поля с узлом-трилистником вокруг тора, ориентированного перпендикулярно направлению распространения света. По мере перемещения света такой узел будет искажаться, но при этом всё время сохранять топологические особенности узла-трилистника. Линии электрического поля имеют ту же структуру, что и линии такого магнитного поля, но сдвинуты относительно оси распространения на угол, который зависит от параметров самого узла. Другие решения уравнений Максвелла дают линии поля, описывающие соединённые между собой кольца и даже пятиконечный узел. Исследователи полагают, что такие узлы для света можно реализовать в лаборатории при помощи лагерровых мод гауссовых пучков — ранее уже создавшихся при изучении возможностей переноса орбитального углового момента и для создания ловушек для ультрахолодных атомов. В принципе, «выстреливая» такими узлами в плазму или квантовую жидкость, можно также добиться создания узлоподобных образований в этих видах материи.
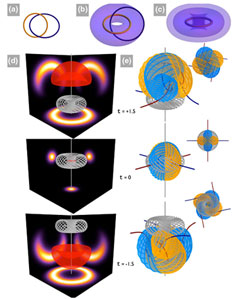 FIG. 1 (color online). Hopfion solution: field line structure (a)–(c) and time evolution (d)–(e). Field lines fill nested tori, forming closed loops linked with every other loop. (a) Hopf link formed by the circle at the core (orange) of the nested tori, and one of the field lines (blue). (b) The torus (purple) that the field line forming the Hopf link is tangent to. (c) Nested tori (purple) enclosing the core, on which the field lines lie. (d) Time evolution of the Poynting field lines (gray), an energy isosurface (red), and the energy density (shown via projections). (e) Time evolution of the electric (yellow), magnetic (blue), and Poynting field lines (gray), with the top view shown in the inset.
FIG. 1 (color online). Hopfion solution: field line structure (a)–(c) and time evolution (d)–(e). Field lines fill nested tori, forming closed loops linked with every other loop. (a) Hopf link formed by the circle at the core (orange) of the nested tori, and one of the field lines (blue). (b) The torus (purple) that the field line forming the Hopf link is tangent to. (c) Nested tori (purple) enclosing the core, on which the field lines lie. (d) Time evolution of the Poynting field lines (gray), an energy isosurface (red), and the energy density (shown via projections). (e) Time evolution of the electric (yellow), magnetic (blue), and Poynting field lines (gray), with the top view shown in the inset.
Статья Hridesh Kedia, Iwo Bialynicki-Birula, Daniel Peralta-Salas, and William T. M. Irvine. Tying Knots in Light Fields опубликована в PHYSICAL REVIEW LETTERS, 111, 150404 (2013)
DOI: 10.1103/PhysRevLett.111.150404
Abstract
We construct analytically, a new family of null solutions to Maxwell’s equations in free space whose field lines encode all torus knots and links. The evolution of these null fields, analogous to a compressible flow along the Poynting vector that is shear free, preserves the topology of the knots and links. Our approach combines the construction of null fields with complex polynomials on S3. We examine and illustrate the geometry and evolution of the solutions, making manifest the structure of nested knotted tori filled by the field lines.
