Физики использовали физические модели из теории магнетизма для анализа результатов выборов
В своей работе, опубликованной в Physical Review Letters, команда описывает модель, в которой присутствуют факторы взаимодействия между избирателями (аналог обменного взаимодействия и анизотропии), которая могла бы как можно точнее предсказать как находящиеся под внешним влиянием (“подмагничивающем поле”) избиратели будут голосовать. Создание же компьютерной модели, которая может точно предсказать исход выборов конечно же является несбыточной мечтой, но на данный этапе исследователи изучают возможность моделирования поведения избирателя находящегося в различных шаблонных ситуациях. Одной из таких ситуаций является склонность избирателей попасть под влияние мнения других людей, будь то люди, которые живут рядом с ними, или же те, с которыми они общаются в рабочее время.
При компьютерном моделировании исследователи свели все факторы воздействия на избирателя к двум: доля республиканцев от демократов в домашнем округе данного избирателя и доля республиканцев от демократов, в том месте, где он работает. Например, избиратель, который обычно голосует за демократов, но если он живет или работает среди республиканцев, в некоторых ситуациях может проголосовать за республиканцев. Модель допускает увеличения или уменьшения расстояния между такими избирателями, чтобы обеспечить усиление или ослабления воздействия, влияющего на голосование.
Таким образом исследователи использовали “шумовую” модель избирателя (то есть попадающего под социальное влияние) с реккурентными мобильными агентами (выступающими в качестве посредников в социальном контексте), где пространственное и популяционное разнообразие взяты в качестве входных параметров модели. Оказалось, что динамика такой модели может быть описана как зашумленный диффузионный процесс, который содержит соответствующую анизотропную топологию, определяемую популяционной и мобильностной неоднородностью. Модель учитывает статистические особенности президентских выборов в США, причем как стационарные колебания количества голосов между округами, так и дальнодействующие пространственные корреляции, падающие экспоненциально с расстоянием. Кроме того, модель позволяет получить поведение этих свойств при укрупнении географических масштабов начиная от городского уровня до избирательного округа и штата. Кроме того, ученые проанализировали роль мобильности и случайности в принятии решений и получили результаты, которые находятся в согласии с эмпирическими наблюдениями.
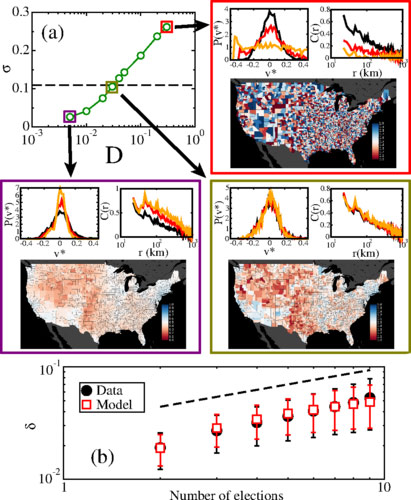
Стандартное отклонение распределения голосов в зависимости от интенсивности шума D. Пунктирной черной линии соответствует дисперсия эмпирических данных (σe=0,11). Приведенные карты получены с уровнем шума отмеченном на основном графике и включают распределение голосов, сдвинутое на нулевое среднее и их пространственную корреляцию. Темные кривые задают начальные условия. Внизу показана средняя дисперсия распределения голосов за демократов в зависимости от номера выборов. Наилучшее согласие с экспериментом получается для значения 2,5 шага Монте-Карло в год.
Источник информации:
