Laboratory of the Theory of Nonlinear Processes
- The Laboratory of the Theory of Nonlinear Processes was grounded in 1973 by Dr. G.M. Zaslavskii. That time, the Laboratory’s topical goal was the theoretical study of chaos in classical nonlinear systems. Currently, the Laboratory is headed by Dr. Almaz F. Sadreev.
Research Focus
- Quantum chaos and its quantum-optical applications in open cavities and elastic billiards.
- Wave transport in linear and nonlinear systems.
- Bloch oscillations and the Wannier--Stark problem.
- Nonlinear dynamics of Bose--Einstein condensates.
- Passage of light in photonic crystal waveguides.
Advanced developments
- We considered the Hall-effect analog in a four-terminal heterostructure due to the Rashba spin-orbit interaction
(E.N. Bulgakov, K.N. Pichugin, A.F. Sadreev, P. Seba and P. Streda, Phys. Rev. Lett. 83, 376-380 (1999);
K.N. Pichugin, P. Streda, P. Seba and A.F. Sadreev, Physica E 6, 727-730 (2000))
- We proved that there is no spin polarization in a two-terminal heterostructure with the Rashba spin-orbit interaction in the case of a single-channel electron transport
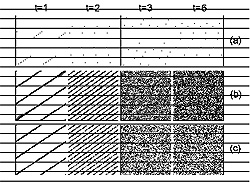
(E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B 66, 075331 (2002)). This result was later confirmed by other authors. - We formulated the quantitative criterion of the correspondence between the classical and quantum chaotic system dynamics (A.R. Kolovsky, Phys. Rev. Lett. 76, 340 (1996)). The Wigner function evolution for the quantum Arnold’s cat map is shown in Fig. 1.
 |
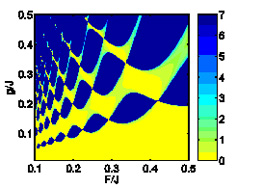 |
| Fig. 1. Wigner function evolution for the quantum Arnold’s cat map in the cases when the conditions of the correspondence are satisfied and unsatisfied. The bottom row shows the distribution function evolution for the classical Arnold’s cat map. | Fig. 2. The number of Bloch-oscillating Bose-condensed atoms as a function of the interatomic interaction and the amplitude of an external static field. |
- We solved the Wannier--Stark problem on the metastable states of a quantum particle in the periodic potential under the action of an external static field (M. Gluck, A.R. Kolovsky, H.J. Korsch, Physics Reports, 366, 103 (2002)).
- We solved the problem on the Bloch oscillations of a Bose condensate of cold atoms in optical lattices (Kolovsky, AR, Korsch, HJ, and Graefe, EM, Phys. Rev. A, 80 023617 (2009)).
- We developed the theory of bound states in the continuum in two-dimensional open billiards, double billiards, Aaronov--Bohm rings, and photonic crystal waveguides coupled with two optical cavities (I. Rotter and A.F. Sadreev, Phys. Rev. E 71, 046204 (2005);
E.N. Bulgakov, K.N. Pichugin, A.F. Sadreev, and I. Rotter, JETP Letters, 84, 430 (2006); A.F. Sadreev, E.N. Bulgakov, and I. Rotter, Phys. Rev. B 73, 235342-5 (2006); E.N. Bulgakov, I. Rotter, and A.F. Sadreev, Phys. Rev. A 75, 67401 (2007);
Chapter in Quantum Dots: Research, Technology and Applications, Ed. by R.W. Knoss, pp. 547-577 (2008, Nova Sci. Publ.);
A.F. Sadreev, E.N. Bulgakov, K.N. Pichugin, I. Rotter, and T.V. Babushkina, Transmission through Quantum Dots with Variable Shape. Bound States in the Continuum;
E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B78, 075105-8 (2008)).
The interest in bound states in the continuum is evoked, first of all, by the proposed interference mechanism of the impurity state localization in the conduction band, in the case when the problem is considered in the scope of the Fano--Anderson model. As applied to the photonic crystal waveguide coupled with two defects, this implies the localization of light near the defects. Examples of such localized solutions for light in a photonic crystal waveguide were reported in Kaleidoscope Phys. Rev. B (2008).
- We investigated self-induced localization of light in a photonic crystal waveguide coupled with optical Kerr cavities (E.N. Bulgakov and A.F. Sadreev, Resonance Induced by a Bound State in the Continuum in a Two-Level Nonlinear Fano--Anderson model, Phys. Rev. B80, 115308-7 (2009);
E.N. Bulgakov and A.F. Sadreev, Bound states in photonic Fabry-Perot resonator comprised of two nonlinear off-channel defects, Pis’ma v ZhETF, 90, 842-847 (2009); E.N. Bulgakov and A.F. Sadreev, Bound States in Photonic Fabry--Perot Resonator with Nonlinear Off-Channel Defects, Phys. Rev. B 81, 115128-12 (2010);
E.N. Bulgakov, K.N. Pichugin, and A.F. Sadreev, Symmetry Breaking for Transmission in Photonic Waveguide Coupled with Two Off-Channel Nonlinear Defects, Phys. Rev. B83, (2011);
E.N. Bulgakov, K.N. Pichugin, and A.F. Sadreev, Light-Induced Josephson-Like Current between Two Nonlinear Cavities Coupled with a Photonic Crystal Waveguide, J. Phys. C23 (2011)).
Among numerous interesting results obtained in this field are the following.
1) At least two different Kerr nonlinear defects pumped by light propagating in a linear waveguide lead to the self-induced light localization (Fig. 3).
2) The localized states, in virtue of the absence of the linear superposition principle, cause additional resonances (Fig. 4).
3) If the defect positions are symmetrical, then the spontaneous symmetry breaking occurs in both the light intensity on the defects and the phase of electromagnetic field oscillations on them. The latter, as is shown in Fig. 5, leads to the Josephson-like effect for a power current.
Fig. 3. Examples of bound states in a two-dimensional photonic crystal fabricated from GaAs cylinders with a radius of 0.18a and a permittivity of 11.56 (light circles). The waveguide is formed simply by removing the rods. The defects are shown by dark circles (E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B 78, 075105 (2008)).
Fig. 4. On the left: transmission in the waveguide coupled with two nonlinear defects parallel to the waveguide (E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B. B80, 115308 (2009)). On the right: in the Fabry--Perot resonator scheme (E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B81, 115128 (2010)).
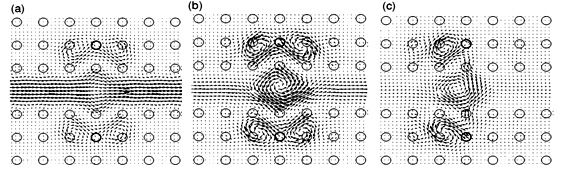
Fig. 5. Light power flows (Umov--Pointing vector) propagating in a waveguide of the photonic crystal near which two identical Kerr defects are located (bold circles). (a) There is no symmetry breaking, (b) symmetry is broken by the light intensity on the defects, and (c) symmetry is broken by the oscillation phase on the defects. One can clearly see the currents between the defects (Josephson currents) in the case of different phases.
- We demonstrated that the spinor Bose--Einstein condensate in an Ioffe-Pritchard magnetic trap can be vortical in the ground state (E.N. Bulgakov and A.F. Sadreev, Phys. Rev. Lett. 90, 200400 (2003)).
- We studied the motion of molecules inside narrow nanotubes under the action of temperature fluctuations of tube walls (A.S. Fedorov and A.F. Sadreev, Thermoactivated Transport of H2 Molecules in Narrow Single-Wall Carbon Nanotubes, Eur. Phys. J. B 69, 363-368 (2009)).
- We developed the theory of quantum chaos for chaotic elastic billiards (D.N. Maksimov and A.F. Sadreev, Gaussian Random Waves in Elastic Media, Pis’ma v ZhETF, 86, 584-588 (2007);
D.N. Maksimov and A.F. Sadreev, Phase Correlation Function of Complex Random Gaussian Fields, Eur. Phys. Lett., 80, 50003 (2007);
Maksimov and A.F. Sadreev, Statistics of Nodal Points of In-Plane Random Waves in Elastic Media, Phys. Rev. E77, 056204-7 (2008)).
